
гии 8 кДж/м3. Направление намагни
ченности также варьировалось. При
d
0
менее 1 мм вносились поправки на су
ществование дефектного слоя в маг
ните толщиной
Δ ≈
0,1 мм с намагни
ченностью
М
= 0.
С помощью программы [3] решалось
уравнение Пуассона для векторного
магнитного потенциала
А
, где
B
= rot
A
, а
B
–индукциямагнитногополя. Для пол
ного определения функции
А
исполь
зовалось условие div
А
= 0, которое яв
лялось калибровкойКулона [4]. Уравне
ние, описывающеемагнитные свойства
материалов конструкции, записыва
лось в виде
B
=
μ
Н
+
B
r
, где
μ
–магнитная
проницаемость вещества, которая яв
лялась функцией |
B
|, т.е. 1/
μ
=
f
|
B
|, что
выражает нелинейнуюсвязь между по
лями
B
и
Н
(напряжённость магнитно
го поля). Тангенциальная составляю
щая
А
= 0 на границе, находящейся в
бесконечности, т.е. достаточно удалён
ной, чтобымагнитнуюэнергиюможно
было принять равной нулю. На оси
симметрии вращения накладывалось
условие
А
= 0, а в плоскостях магнит
ной и геометрической симметрии –
dА
/
dn
= 0, т.е. линии потока перпенди
кулярны этим плоскостям.
Область расчета магнитного поля
выбиралась как минимум на два по
рядка больше характерных размеров
(длин 2
a
). Она разбивалась на конеч
ные элементы задаваемых размеров.
Как правило, элементы, используемые
для дискретизации рассматриваемой
области, имели вид треугольников,
причём их размеры увеличивались
при приближении к границам модели
в бесконечности. В областях, прибли
женных к магнитам, число точек дис
кретизации принудительно увеличи
валось. В остальной области расчёта
дискретизация выполнялась автома
тически. Общее количество точек, в
которых осуществлялся расчёт, состав
ляло не менее 30 – 50 тыс. Постпро
цессор решал систему линейных ал
гебраических уравнений до тех пор,
пока сходимость уравнений не дости
гала10
–8
.
Для задания свойств магнитных ма
териалов использовалась встроенная
в программу femm библиотека. Для
материалов российского производ
ства параметры вводились вручную в
соответствии с выбранными лите
ратурными источниками. На рис. 3–5
в основном приведены значения
В
n
составляющей индукции магнитно
го поля в зависимости от длины пе
ремещения по координате Y вооб
ражаемого датчика Холла. Начало
перемещения 0 мм каждый раз зада
валось вручную, исходя из длины пе
ремещения моделируемого элемен
та Холла.
Изменение расстояния прохожде
ния
L
элемента Холла над магнитами
приводит к типичным изменениям
В
n
,
как показано на рисунке 4. Следует от
метить, что при таком расположении
магнитов датчик может работать в
очень узкой области вблизи смены
магнитных полюсов, где очень высо
кий градиент
В
n
(см. рис. 5), и такая
конструкция фактически выполняет
функцию магнитного репера.
В таблице приведены средние зна
чения градиента индукции магнит
ного поля
В
n
репера вблизи смены по
люсов магнитов (SmCo
5
20MGOe,
d
0
=
= 0,0 мм;
Δ
= 0,1 мм). База расчёта гради
ента составляет 200 мкм при различ
ных геометрических размерах.
В результате анализа полученных
расчётных и экспериментальных дан
ных о распределении компонентов ин
дукции магнитного поля можно сфор
мулировать рекомендации по оптими
зации конструкция репера:
●
для получения максимальной чувст
вительности элемента Холла к пере
мещениюв зоне сменыполюсов маг
нитной системырепера необходимо
расположить миниатюрные магни
ты с нулевым расстояниеммежду ни
ми (соприкасающимися), а расстоя
ние между линией движения датчика
Холла и репером выбрать минималь
но возможным, т.е. с учётом отсут
ствия механического контакта, в ди
апазоне 0,5 ± 0,1 мм;
●
для получения высокого градиента
магнитного поля в области смены
полюсов репера необходимо ис
пользовать магниты, изготовленные
из закритических материалов и об
ладающие высокими значениями
удельной магнитной энергии и без
дефектнойприповерхностной струк
турой.
Врезультате компьютерногомодели
рования различных вариантов испол
нения репера, включавших как выбор
ПРОЕКТИРОВАНИЕ И МОДЕЛИРОВАНИЕ
42
WWW.SOEL.RUСОВРЕМЕННАЯ ЭЛЕКТРОНИКА
◆
№ 6 2011
–0,4
–0,3
–0,2
–0,1
0
0,1
0,2
0,3
0,4
Bn, Тл
0
5
10
Длина, мм
Рис. 4. Распределение нормальной
составляющей индукции магнитного поля
B
n
магнитной системы из двух магнитов при
a
=
c
=
= 5,0 мм;
d
0
= 0,0 мм;
Δ
= 0,1 мм и
L
= 0,5 мм;
магниты марки SmCo
5
20MGOe
–0,1
–0,05
0
0,05
0,1
Bn, Тл
0
0,1 0,2 0,3 0,4 0,5 0,6
Длина, мм
Рис. 5. Распределение нормальной
составляющей индукции магнитного поля
B
n
репера вблизи смены полюсов магнитов
при
a
=
c
= 5,0 мм;
d
0
= 0,0 мм;
Δ
= 0,1 мм
и
L
= 1,0 мм; магниты марки SmCo
5
20MGOe
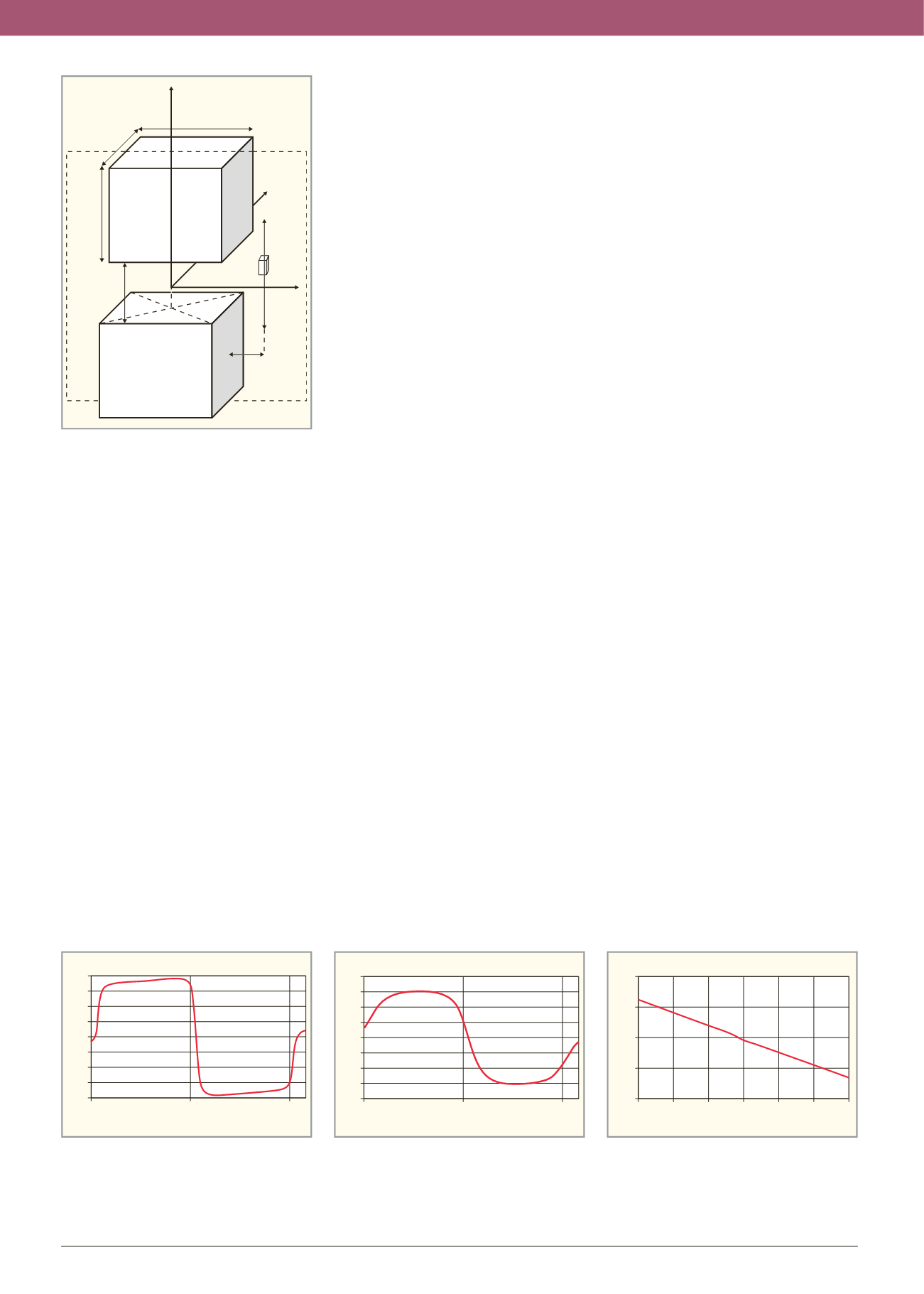
Y
Z
X
L
d
0
c
g
π
S
S
N
N
a
Рис. 2. Магнитная система из двух магнитов типа
«магнитный репер»
–0,4
–0,3
–0,2
–0,1
0
0,1
0,2
0,3
0,4
Bn, Тл
0
5
10
Длина, мм
Рис. 3. Распределение нормальной
составляющей индукции магнитного поля
B
n
магнитной системы из двух магнитов при
a
=
c
=
= 5,0 мм;
d
0
= 0,0 мм;
Δ
= 0,1 мм и
L
= 0,0 мм;
магниты марки SmCo
5
20MGOe
© СТА-ПРЕСС


















